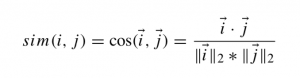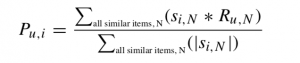Für ein Projekt an der Uni beschäftige ich mich seit längerer Zeit mit Empfehlungssystemen (Recommender Systems), welche i.d.R. aus Collaborative Filtering und Content-Based Recommendation Techniken bestehen.
In diesem Blogpost möchte ich auf die Collaborative Filtering-Komponente, genauer auf das Item-Based Collaborative Filtering eingehen. Das Item-Based Collaborative Filtering wurde ursprünglich von Amazon entwickelt. “Traditionelles” Collaborative Filtering, besser bekannt als “User-Based CF”, repräsentiert einen User als einen n-dimensionalen Item-Vektor und misst deren Ähnlichkeit. User-Based Ansätze sind sehr rechenintensiv, in O-Notation ausgedrückt wäre sie O(MN), wobei M die Anzahl der Benutzer und N die Anzahl der Items darstellt.
Amazon stellt in “Amazon.com Recommendations – Item-to-Item Collaborative Filtering” fest, dass in der Praxis zwar die meisten User nur einen bestimmten Anteil der Items gekauft/bewertet haben, dies aber trotzdem ein Problem aus Sicht der Performance bzw. Komplexität darstellt. Selbst das Aufteilen in Produkt-/User-Kategorien schaffen nur bedingt Abhilfe. Ferner führt dies dazu, dass die Empfehlungen zu ungenau werden.
Item-Based Collaborative Filtering
Jeder kennt den “Customer who bought this item also bought”-Abschnitt auf Amazon. Dabei verwendet Amazon verschiedene Algorithmen um Empfehlungen für Nutzer zu personalisieren. Um der großen Benutzer- und Produktpalette – technischer ausgedrückt: der riesigen Datenmenge – der eigenen Plattform einen geeigneten Ansatz zu finden, hat Amazon seinen eigenen Algorithmus entwickelt: Item-to-Item oder Item-Based Collaborative Filtering. Amazon beschreibt den Algorithmus mit den Worten “skaliert riesige Datenmengen und berechnet Empfehlungen in Echtzeit”.
Anstelle ähnliche Benutzer zu einem gegebenen User zu finden, sucht das Item-Based CF nach ähnlichen Produkten zu einem Produkt, die der User bewertet/gekauft hat und kombiniert diese Produkte zu einer “Recommendation List”.
Zunächst wird eine Tabelle mit Artikeln erstellt, bei dem jeder Artikel von verschiedenen Benutzer bereits gekauft wurde. Eine Produkt-Produkt-Matrix mit einer Berechnung der Ähnlichkeit wäre hier zwar denkbar, aber gegeben durch den Fakt, dass die meisten Produktpaare keine gemeinsamen Benutzer haben, wäre der Ansatz ineffizient. Stattdessen wird jedes Produkt einzeln, aber mit Bezug auf die bereits gekauften betrachtet.
| n1 | n2 | n3 | |
| m1 | 0 | 0 | 0 |
| m2 | 1 | 1 | 1 |
| m3 | 1 | 0 | ? |
Gegeben ist hier eine User-Item-Matrix in der jeder Benutzer m ein Produkt n bewertet bzw. gekauft hat. Lediglich User m3 hat für n3 noch keine Bewertung abgegeben, die es nun vorherzusagen gilt. Dieser Vorhersage (Prediction) wird anschließend genutzt um zu entscheiden, ob der Artikel dem Benutzer vorgeschlagen werden soll oder nicht.
Ähnlichkeit durch Cosine Similarity
Doch zunächst muss die Ähnlichkeit zwischen n1 und n3, n1 und n2 und n2 und n3 berechnet werden. Hierfür sind verschiedene Ansätze vorhanden. Wir wählen hier die Cosine Similarity, die auch von Amazon erwähnt wird:
i und j sind Vektoren, die zwei Produkte mit ihren Bewertungen darstellen und das “·” für das Skalarprodukt beider Vektoren. Ausgehend von dieser Formel würde unsere Berechnung also wie folgt aussehen:
cos(n1,n3) = (0 * 0) + (1 * 1) / sqrt[(0+1)²] * sqrt[(0+1)²] = 0 + 1 / sqrt[1] + sqrt[1] = 1 / 1 = 1
cos(n1,n2) = (0 * 0) + (1 * 1) + (1 * 0) / sqrt[(0+1+1)²] * sqrt[(0+1+0)²] = 1 / 2 = 0,5
cos(n2,n3) = (0 * 0) + (1 * 1) / sqrt[(0+1)²] * sqrt[(0+1)²] = 0 + 1 / sqrt[1] + sqrt[1] = 1 / 1 = 1
Folglich ergibt sich die folgende Ähnlichkeitsmatrix:
| n1 | n2 | n3 | |
| n1 | 1 | 0,5 | 1 |
| n2 | 0,5 | 1 | 1 |
| n3 | 1 | 1 | 1 |
Prediction
Unsere Ausgangsfrage, die Bewertung m3 für n3, steht noch immer offen. Um diese zu berechnen können ebenfalls verschiedene Ansätze verfolgt werden. Nachfolgend die “gewichtete Summe” (weighted sum):
Zunächst muss definiert werden welche Produkt dem gesuchten Produkt n3 “ähnlich” sind. Denkbar wäre z.B. ein definierter Threshold. Zur Einfachheit gehen wir davon aus, dass sowohl n1 als auch n2 ähnlich genug zu n3 sind um sie für die oben gezeigte Formel in Betracht zu ziehen:
P (u,i) = (1 * 1)+(1 * 0) / 1 + 0 = 1
Fazit
Die obigen Werte User-Bewertungen sind binär, d.h. der Benutzer hat entweder ein Produkt gekauft, geliked, angesehen, etc. Die gleiche Formel kann man natürlich auch für eine definierte Skala, z.B. 1-5, anwenden.
Die ersten Tests auf Papier haben bei mir durchaus positive Ergebnisse ergeben. Selbst die Komplexität hält sich in Grenzen (verglichen zu anderen Formeln). Nun gilt es, das oben beschriebene in Form von Source Code nachzubauen. Dies wird aber etwas Zeit in Anspruch nehmen. Ich berichte…
Zum Weiterlesen:
- https://www.cs.umd.edu/~samir/498/Amazon-Recommendations.pdf
- https://ashokharnal.wordpress.com/2014/12/18/worked-out-example-item-based-collaborative-filtering-for-recommenmder-engine/